杭电ACM 解题报告 - neuxxm's Blog - 本为贵公子,平生实爱才。感时思报国,拔剑起蒿莱。
杭电ACM 1028 Ignatius and the Princess III
Ignatius and the Princess III
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4193 Accepted Submission(s): 2931
"The second problem is, given an positive integer N, we define an equation like this:
N=a[1]+a[2]+a[3]+...+a[m];
a[i]>0,1<=m<=N;
My question is how many different equations you can find for a given N.
For example, assume N is 4, we can find:
4 = 4;
4 = 3 + 1;
4 = 2 + 2;
4 = 2 + 1 + 1;
4 = 1 + 1 + 1 + 1;
so the result is 5 when N is 4. Note that "4 = 3 + 1" and "4 = 1 + 3" is the same in this problem. Now, you do it!"
4 10 20
5 42 627
#include <stdio.h> #include <string.h> #define N 120 int c1[N+1], c2[N+1]; int main(){ int i, j, k, n; for (i=0; i<=N; ++i){ c1[i] = 1; } for (k=2; k<=N; ++k){ memset(c2, 0, sizeof(c2)); for (i=0; i<=N; ++i){ for (j=i; j<=N; j+=k){ c2[j] += c1[i]; } } memcpy(c1, c2, sizeof(c2)); } while (scanf("%d", &n) == 1){ printf("%d\n", c1[n]); } return 0; }
杭电ACM 1021 Fibonacci Again
Fibonacci Again
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 14170 Accepted Submission(s): 6581
Print the word "no" if not.
0 1 2 3 4 5
no no yes no no no
#include <stdio.h> int main(){ int n, t; while (scanf("%d", &n) == 1){ t = n&7; printf("%s\n", t==2 || t==6 ? "yes" : "no"); } return 0; }
杭电ACM 1019 Least Common Multiple
Least Common Multiple
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10956 Accepted Submission(s): 3953
2 3 5 7 15 6 4 10296 936 1287 792 1
105 10296
#include <stdio.h> int gcd(int x, int y){ if (y == 0){ return x; } int i = x&1, j = y&1; return i ? j ? (x>y ? gcd(y, x-y) : gcd(x, y-x)) : gcd(x, y>>1): j ? gcd(x>>1, y) : gcd(x>>1, y>>1)<<1; } int lcm(int x, int y){ return x/gcd(x, y)*y; } int main(){ int z, n, t, r; scanf("%d", &z); while (z-- != 0){ scanf("%d", &n); scanf("%d", &r); while (--n != 0){ scanf("%d", &t); r = lcm(r, t); } printf("%d\n", r); } return 0; }
杭电ACM 1017 A Mathematical Curiosity
A Mathematical Curiosity
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10170 Accepted Submission(s): 3078
This problem contains multiple test cases!
The first line of a multiple input is an integer N, then a blank line followed by N input blocks. Each input block is in the format indicated in the problem description. There is a blank line between input blocks.
The output format consists of N output blocks. There is a blank line between output blocks.
1 10 1 20 3 30 4 0 0
Case 1: 2 Case 2: 4 Case 3: 5
#include <stdio.h> int a2b2[101][101]; int ab[101][101]; int a[101]; int main(){ int zz, z, n, m, i, j, b, r; for (i=1; i<=100; ++i){ a[i] = i*i; } for (i=1; i<=100; ++i){ for (j=1; j<=100; ++j){ a2b2[i][j] = a[i]+a[j]; ab[i][j] = i*j; } } b = 0; scanf("%d", &zz); while (zz-- != 0){ if (b){ printf("\n"); } b = 1; z = 0; for (;;){ scanf("%d %d", &n, &m); if (n==0 && m==0){ break; } r = 0; for (i=1; i<n; ++i){ for (j=i+1; j<n; ++j){ if ((a2b2[i][j]+m)%ab[i][j] == 0){ ++r; } } } printf("Case %d: %d\n", ++z, r); } } return 0; }
杭电ACM 1014 Uniform Generator
Uniform Generator
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5668 Accepted Submission(s): 2252
seed(x+1) = [seed(x) + STEP] % MOD
where '%' is the modulus operator.
Such a function will generate pseudo-random numbers (seed) between 0 and MOD-1. One problem with functions of this form is that they will always generate the same pattern over and over. In order to minimize this effect, selecting the STEP and MOD values carefully can result in a uniform distribution of all values between (and including) 0 and MOD-1.
For example, if STEP = 3 and MOD = 5, the function will generate the series of pseudo-random numbers 0, 3, 1, 4, 2 in a repeating cycle. In this example, all of the numbers between and including 0 and MOD-1 will be generated every MOD iterations of the function. Note that by the nature of the function to generate the same seed(x+1) every time seed(x) occurs means that if a function will generate all the numbers between 0 and MOD-1, it will generate pseudo-random numbers uniformly with every MOD iterations.
If STEP = 15 and MOD = 20, the function generates the series 0, 15, 10, 5 (or any other repeating series if the initial seed is other than 0). This is a poor selection of STEP and MOD because no initial seed will generate all of the numbers from 0 and MOD-1.
Your program will determine if choices of STEP and MOD will generate a uniform distribution of pseudo-random numbers.
3 5 15 20 63923 99999
3 5 Good Choice
15 20 Bad Choice
63923 99999 Good Choice
#include <stdio.h> int gcd(int x, int y){ if (y == 0){ return x; } int i = x&1, j = y&1; return i ? j ? (x>y ? gcd(y, x-y) : gcd(x, y-x)) : gcd(x, y>>1) : j ? gcd(x>>1, y) : gcd(x>>1, y>>1)<<1; } int main(){ int x, y; while (scanf("%d %d", &x, &y) == 2){ printf("%10d%10d %s\n\n", x, y, gcd(x, y)==1 ? "Good Choice" : "Bad Choice"); } return 0; }
杭电ACM 1013 Digital Roots
Digital Roots
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 19299 Accepted Submission(s): 5632
For example, consider the positive integer 24. Adding the 2 and the 4 yields a value of 6. Since 6 is a single digit, 6 is the digital root of 24. Now consider the positive integer 39. Adding the 3 and the 9 yields 12. Since 12 is not a single digit, the process must be repeated. Adding the 1 and the 2 yeilds 3, a single digit and also the digital root of 39.
24 39 0
6 3
#include <stdio.h> int f(int n){ if (n <= 9){ return n; } int r = 0; while (n > 0){ r += n%10; n /= 10; } return f(r); } int main(){ char s[1025]; int i, n; while (scanf("%s", s) == 1){ n = 0; for (i=0; s[i]; ++i){ n += s[i]-'0'; } if (n == 0){ break; } printf("%d\n", f(n)); } return 0; }
杭电ACM 1012 u Calculate e
u Calculate e
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 11752 Accepted Submission(s): 5028
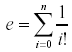
where n is allowed to go to infinity. This can actually yield very accurate approximations of e using relatively small values of n.
n e - ----------- 0 1 1 2 2 2.5 3 2.666666667 4 2.708333333
#include <stdio.h> int main(){ double sum; int n, i, l; printf("n e\n"); printf("- -----------\n"); printf("0 1\n"); sum = 1; l = 1; for (n=1; n<=9; ++n){ l *= n; sum += 1.0/l; if (n <= 2){ printf("%d %g\n", n, sum); } else{ printf("%d %.9lf\n", n, sum); } } return 0; }
杭电ACM 1008 Elevator
Elevator
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 15522 Accepted Submission(s): 8168
For a given request list, you are to compute the total time spent to fulfill the requests on the list. The elevator is on the 0th floor at the beginning and does not have to return to the ground floor when the requests are fulfilled.
1 2 3 2 3 1 0
17 41
#include <stdio.h> int main(){ int n, t, l, r; while (scanf("%d", &n) == 1){ if (n == 0){ break; } r = 0; l = 0; while (n-- != 0){ scanf("%d", &t); if (t > l){ r += (t-l)*6; } else{ r += (l-t)*4; } r += 5; l = t; } printf("%d\n", r); } return 0; }
杭电ACM 1005 Number Sequence
Number Sequence
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 38553 Accepted Submission(s): 8150
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
Given A, B, and n, you are to calculate the value of f(n).
1 1 3 1 2 10 0 0 0
2 5
#include <stdio.h> #include <string.h> int main(){ int b[7][7]; int a[100]; int n; int x, y, m, st, len; while (scanf("%d %d %d", &x, &y, &m) == 3){ if (x==0 && y==0 && m==0){ break; } a[1] = 1; a[2] = 1; memset(b, 0, sizeof(b)); b[1][1] = 1; n = 3; for (;;){ a[n] = (a[n-1]*x+a[n-2]*y)%7; if (b[a[n-1]][a[n]] != 0){ break; } b[a[n-1]][a[n]] = n-1; ++n; } st = b[a[n-1]][a[n]]; len = n-1-st; if (m < st){ printf("%d\n", a[m]); } else{ printf("%d\n", a[st+(m-st)%len]); } } return 0; }
杭电ACM 1004 Let the Balloon Rise
Let the Balloon Rise
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 28869 Accepted Submission(s): 9266
This year, they decide to leave this lovely job to you.
A test case with N = 0 terminates the input and this test case is not to be processed.
5 green red blue red red 3 pink orange pink 0
red pink
#include <stdio.h> #include <string.h> #define N 390 const char C = 'a'-1; struct bal_t{ char color[16]; int fre; }bal[N+1]; int hash(char s[]){ int r = 0; char *p = s; char c; while ((c=*p++) != '\0'){ r += c-C; } return r; } int main(){ char s[16]; int n, i, t, max, max_i; while (scanf("%d", &n) == 1){ if (n == 0){ break; } for (i=0; i<=N; ++i){ bal[i].fre = 0; } while (n-- != 0){ scanf("%s", s); t = hash(s); if (bal[t].fre != 0){ ++bal[t].fre; } else{ strcpy(bal[t].color, s); bal[t].fre = 1; } } max = 0; for (i=0; i<=N; ++i){ if (bal[i].fre > max){ max = bal[i].fre; max_i = i; } } printf("%s\n", bal[max_i].color); } return 0; }